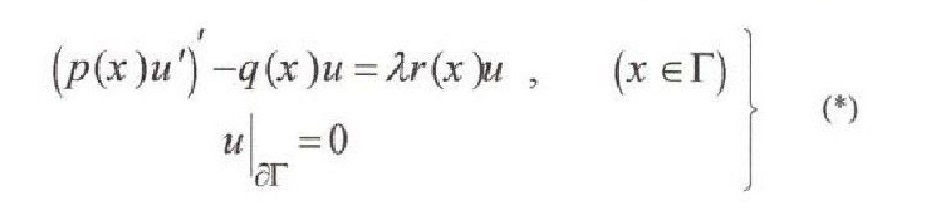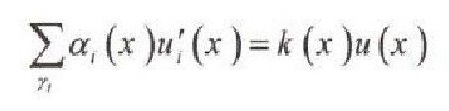آخر الأخبار
التكرار الهندسي لطيف مسألة ديرخليه (غير الملساء) على البيان الهندسي
2011, Volume 4, issue 16,pp 37-49| Cite as
Geometric multiplicity of spectrum for the discontinuous dirichlet problem on a geometric graph
| authors |
Mounir Turk |
| Abstract |
Consider, on the geometric graph Г, the spectral boundary value problem
Where p , q and r are the positive functions, q is the real valued function and λ is a spectral parameter. Suppose that function u satisfies a boundary condition in every internal node a of Г
Where a1 (x) and k (x) are fixed and positive numbers. The summation is performed over the edges y1 adjoin to the vertex x and u1(x ) denotes the "boundary" derivative of u at the end x of the edges Y1 in the direction "from x". We study with the problem(*) the problem (*1) replacing Г by Г, where Г, is the component of the connected set r{c} where c is an internal node of r; j = 1,2,...,/. Suppose that x(λ) is a geometric multiple for λ as an eigenvalue for the problem (*) and X1(λ) is a geometric multiple for à as an eigenvalue for the problem (*1). Then the difference
equals 0 or -1 .
Key words: Dirichlet problem, eigenvalue, Graph. |
| الكاتب |
منير الترك |
| الملخص |
ندرس على البيان الهندسي Г، مسألة القيم الحدية الطيفية:
حيث p وq و r دوال ذات قيم حقيقية وp و r دوال موجبة و λ وسيط طيفي . نفرض أن الدالة u تحقق في العقد الداخلية للبيان Г الشرط: حيث (a1(x و (k(x أعداد موجبة، والمجموع محسوب على كل الأضلاع y1 التي لها الطرف x و (u1(x مشتق الدالة u عند x على الضلع y1، بالاتجاه من x ندرس بالتوافق مع المسألة (*) المسألة (1*)، الناتجة عن المسألة (*) باستبدال Г بـ ,Г الذي يعبر عن أحد التراكيب المترابطة من المجموعة { Г/(c)حيث Cعقدة داخلية للبيان Г و j=1,2,...,1 نفرض (x(λ تكرار هندسي للقيمة الذاتية λ للمسألة (*) و (x1(λ تكرارهندسي للقيمة الذاتية نفسها λ للمسألة (1*). عندئذ يكون الفرق
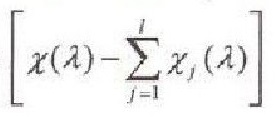 مساويا للصفر أو ناقص واحد.
الكلمات المفتاحية: مسألة ديريخليه، قيمة ذاتية، بيان. |