جامعة الفرات
حول التقريب المنتظم لـ xn في فضاء كثيرات الحدود الجبرية Pn-1
الباحث الرئيسي: جمال مللي ، صفوان زيزون ،رهف الدكاك
ملخص البحث (Abstract)
يعد الرياضي الروسي تشيبتشيف مؤسس نظرية التقريب المنتظم ،وقد قام بإيجاد حدودية التقريب الأمثل من الدرجة n-1 للدوال 
في كل من الفضائين [C[-1,1 و[C[0,1 ،وذلك بواسطة حدوديات تشيبتشيف.
و قد قمنا في هذا العمل بإيجاد حدودية التقريب الأمثل لهذه الدوال في فضاء كثيرات الحدود الجبرية Pn-1 ولكن على المجالات [a,a-] و [a,0] ومن ثمّ استفدنا من متناوبات تشيبتشيف لهذه الدوال ومن خواص الدالة العكسية في إيجاد متناوبات الدوال ذات الشكل :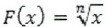 
على المجال [0,a] إذا كان n عدداً طبيعياً،و على المجال [a,a-] إذا كان n عدداً طبيعياً فردياً ,و من ثمّ إيجاد حدودية التقريب الأمثل لهذه الدّوال في الفضاء على تلك المجالات .
على المجال [0,a] إذا كان n عدداً طبيعياً،و على المجال [a,a-] إذا كان n عدداً طبيعياً فردياً ,و من ثمّ إيجاد حدودية التقريب الأمثل لهذه الدّوال في الفضاء على تلك المجالات .الكلمات المفتاح : دالة مستمرة -حدودية التقريب الأمثل – كثيرات حدود تشيبتشيف متناوبات تشيبتشيف- الدالة العكسية.
طريقة الاقتباس (APA) (APA)
جمال مللي ، صفوان زيزون ،رهف الدكاك. (2012). حول التقريب المنتظم لـ xn في فضاء كثيرات الحدود الجبرية Pn-1. مجلة جامعة الفرات للبحوث والدراسات العلمية, 6(1), pp. 184-199.